Mouvement d’une particule chargée dans un champ magnétique

I Etude expérimentale :

1-1  Observation d’une vidéo

Cliquer sur le lien suivant pour visionner la vidéo

Mouvement d'une particule chargée dans un champ magnétique (vidéo « déviation magnétique.avi »)

Observer le clip et l’interpréter.

Quelle(s) informations apporte cette expérience?

1-2 Recherche d’une expression de la force magnétique :

En l’absence de matériel, nous proposons d’utiliser une simulation.

La figure ci-dessous indique les différents paramètres modifiables pouvant influer sur la force .Vous pouvez tester l’effet de chacun d’eux sur le mouvement d’une particule (électrisée ou non)

Soit OXYZ un repère cartésien .

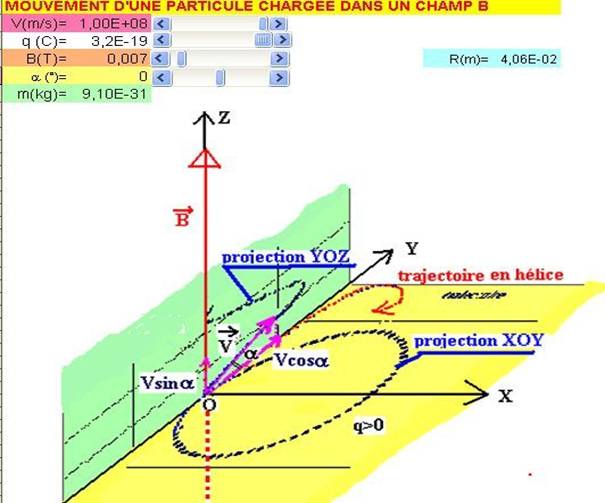
Les particules pénètrent dans le champ en O avec un vecteur vitesse V (d’intensité  réglable) qui appartient au plan YOZ et incliné de a (réglable de -90° à +90°) par rapport à l’axe OY.

Le champ magnétique ici est uniforme .Il est caractérisé par le vecteur B orienté suivant l’axe OZ. Seule sa valeur B est réglable.

Il faut sélectionner la charge q et la masse m de la particule

Il est possible de choisir les charges suivantes :

q=+2e ; q=+e ; q=0 ; q=-e ; q=-2e (avec e=1,6.10^-19C).

Effectuer les réglages proposés dans le tableau ci-dessous. Aprés observation des conséquences sur le mouvement, donner les informations sur la force .

(compléter le tableau : il peut être utile de recopier celui-ci sur une feuille annexe )

Cliquer sur le lien suivant pour accéder à la simulation proposée.

Mouvement d'une particule dans B(document Excel) 

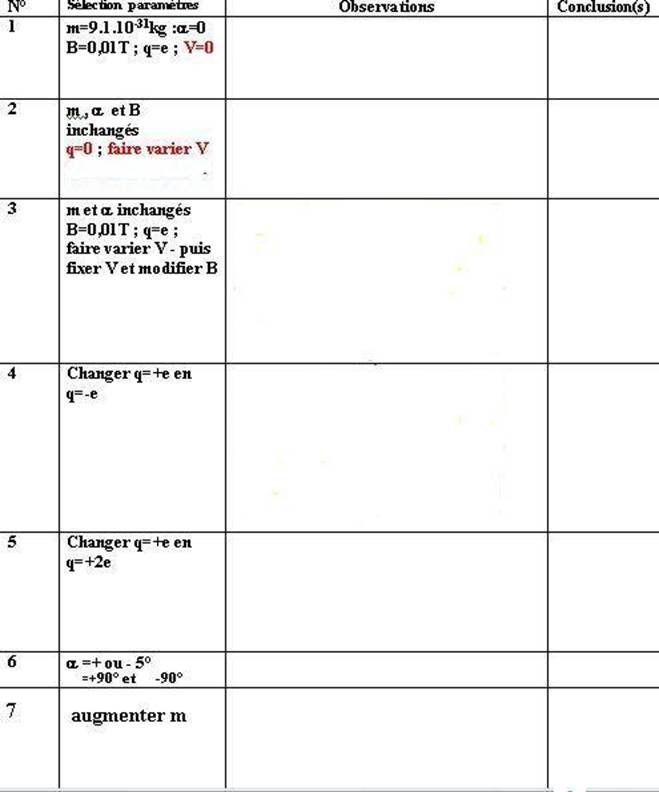
Après avoir complété le tableau, on pourra éventuellement consulter les réponses proposées à la fin de ce texte

II-Etude théorique :

a-la force de Lorentz

L’hypothèse de Lorentz. :une particule électrisée de charge q  pénètrant dans un champ magnétique B avec une vitesse V  est soumise  à la force magnétique :

:

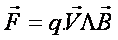
Les caractéristiques de cette force sont (en accord avec les propriétés du produit vectoriel):

-la direction : elle est perpendiculaire au plan qui contient v et B.

-le sens de F dépend du signe de q :

Si q>0, le sens de F est tel que le trièdre v, B, F soit direct.

Si q<0, le trièdre est indirect.(voir figure ci-dessous )

-son intensité est : F=|q|.v.B.sin(a) (a étant l’angle entre les vecteurs v et B).

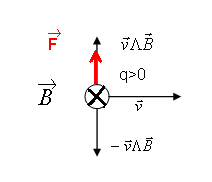
La « règle de la main droite » permet de retrouver facilement le sens de la force F.

Placer la main dans la direction de v (l’extrémité des doigts correspondant au sens de la flèche), la paume de la main « regardant » le champ B « s’éloigner », le pouce indique  le sens du produit vectoriel (vLB).

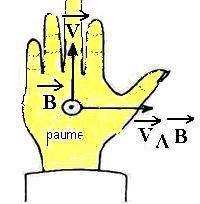
Si q>0, la force F a même sens que (vLB).

Si  q<0, la force F a le sens contraire de ( vLB).

b-mouvement d’une particule chargée :

Nous considérons le référentiel galiléen.

1-si v//B , la force de Lorentz est nulle et donc le vecteur vitesse reste constant. Le mouvement est rectiligne et uniforme

2-si v est perpendiculaire à B :

Envisageons le cas d’un électron (de charge q<0), qui pénètre à t=0 avec une vitesse v_o dans le champ B .(voir figure)

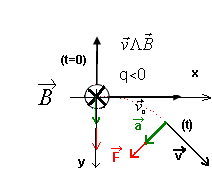La 2^ème loi de Newton permet d’écrire :

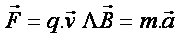
Soit :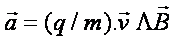 

La force F est normale à la vitesse et à B, elle appartient donc au plan xOy, la trajectoire appartient aussi à ce plan. L’accélération a est normale au vecteur vitesse v.

Les composantes normale (orientée vers l’intérieur de la trajectoire)  et tangentielle de l’accélération sont :

a_T=0=dv/dt  et donc v=cte, le mouvement est donc uniforme.

a_N=|q|v₀B/m=v²/R la trajectoire est circulaire de rayon :

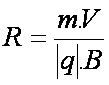
Application numérique :

Q=-1,6 10-19C ; m=9.1 10-31kg ; V=4,4.107 m.s-1 ; B=0.010T

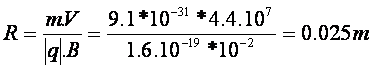
Valeur en accord avec les observations

Réponses possibles aux questions de la partie expérimentale :

1-Observations du clip vidéo 

Remarque :la tension de 5000V est une tension accélératrice. Nous devons donc supposer que les électrons pénètrent dans l’ampoule avec une certaine vitessse. Malheureusement les 2 bobines latérales ne sont pas alimentées. Aucune sollicitation de ces bobines n’est donc à envisager  !

A l’approche de l’aimant, la trajectoire des électrons est  modifiée .Ceci permet de  d’affirmer qu’une force de nature magnétique s’exerce sur les électrons.

L’inversion des pôles  de l’aimant modifie le sens de la déviation.

Le sens de la force de déviation dépend donc  du sens de B. 

Il est difficile, par cette expérience, de relier les caractéristiques de la force au vecteur champ, celui-ci n’étant pas uniforme.(la direction du champ est mal connue au niveau du faisceau d’électrons).Une étude plus complète est nécessaire

2-Résultats de  la simulation :

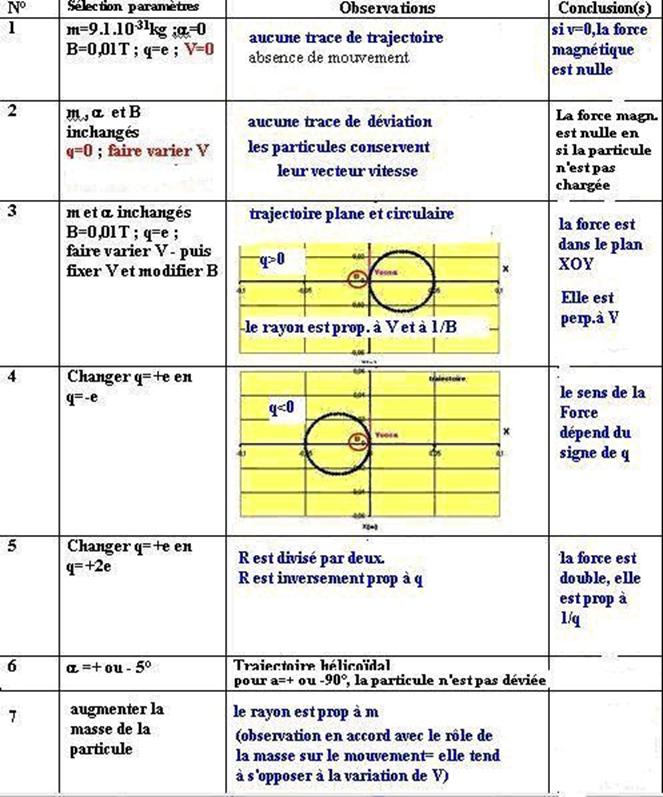
Cette simulation permet aussi de valider les exercices sur le sujet.